Here is a list of interview questions for senior full-stack engineers, covering basic knowledge, front-end, back-end, and architecture. It is a classic set of questions that never goes out of style.
Computer Networking #
CIDR #
How many available IP addresses are there in the following CIDR address block?
#
10.0.0.0/24
2^(32-24)-2=2^8-2=254
What is the corresponding IP address range? #
10.0.0.1 ~ 10.0.0.254
10.0.0.0 is not assignable, it is the starting address of the subnet.
10.0.0.255 is not assignable, it is the broadcast address of the subnet.
Subnetting #
With the following subnet mask and two IP addresses, are they in the same subnet? #
255.255.255.0
192.168.0.10
192.168.1.10
No, because the result of the AND operation between the two IP addresses and the subnet mask is different. They are:
192.168.0.10 & 255.255.255.0 = 192.168.0.0
192.168.1.10 & 255.255.255.0 = 192.168.1.0
Default Gateway #
The default gateway is a network device used to send packets from one network to another. When a device wants to send a packet to another network, it checks if the destination IP address is in the same subnet.
- If it is, the device can communicate directly without going through the gateway.
- If it is not, the device sends the packet to the default gateway, which forwards it to the destination network.
The default gateway is usually a router that connects two different networks.
NAT #
Network Address Translation (NAT) is a technology that converts private IP addresses into public IP addresses. In a
private subnet, each device has only one private IP address and cannot communicate directly with the Internet. NAT maps
private IP addresses to a single public IP addresses.
UDP VS TCP #
In simple terms, TCP is a connection-oriented, reliable, ordered, byte-stream transport protocol. UDP is a
connectionless, unreliable, unordered, packet-based transport protocol.
| Feature | TCP | UDP |
|---|---|---|
| Connection | Connection-oriented | Connectionless |
| Reliability | Reliable due to error checking, retransmission, reassembling | Unreliable due to no error checking and retransmission, reassembling |
| Speed | Slower due to overhead | Faster due to no overhead |
| Flow/Congestion control | Yes | No |
| Header size | Larger (20 - 60 bytes) | Smaller (8 bytes) |
| Use case | Web browsing, file transfer, email | Real-time application like video streaming, online gaming, VoIP (voice over IP) |
DNS #
A Record #
An
Arecord maps a domain name to an IPv4 address. The@symbol represents the root domain.
| example.com | record type | value | TTL |
|---|---|---|---|
| @ | A | 192.0.2.1 | 14400 |
CNAME #
A
CNAMErecord is an alias for a domain name. It maps one domain name to another. For example:
| blog.example.com | record type | value | TTL |
|---|---|---|---|
| @ | CNAME | is an alias of example.com | 32600 |
HTTP #
Why need three-way handshake for establishing a connection? #
- The first time proves that the client can send data (SYN).
- The second time proves that the server can receive data and send data (SYN + ACK).
- The third time proves that the client can receive data (ACK).
It is like making a phone call. A says, “Can you hear me?” B says, “I can hear you, can you hear me?” A says, “I can hear you too.”
Why need four-way handshake for closing a connection? #
- The first time the client tells the server that the client will no longer send data (FIN).
- The second time the server tells the client that the server still has data to send (ACK).
- The third time the server tells the client that the server will no longer send data (FIN).
- The fourth time the client tells the server that it can close the connection (ACK).
Because TCP is full-duplex, closing a connection requires two steps. It is like ending a phone call. A says, “I’m done talking.” B says, “I still have something to say.” B says, “I’m done talking.” A says, “Okay.”
Is there a limit to the length of a URL? #
The HTTP protocol does not specify a maximum URL length, but browsers and servers have limits. For example, Chrome’s URL length limit is 2KB.
How to disable browser caching? #
You can disable browser caching by setting the HTTP response headers, including:
Cache-Control: no-cache, no-store, must-revalidate
Pragma: no-cache
Expires: 0
- Cache-Control
no-cachemeans do not cache,no-storemeans do not store,must-revalidatemeans must revalidate. - Pragma
no-cachemeans do not cache (HTTP/1.0). - Expires set to 0 means expire immediately (HTTP/1.0).
CORS #
CORS (Cross-Origin Resource Sharing) is a security feature enforced by browsers to prevent malicious websites from
making requests to another origin without permission. However, CORS does not affect server-to-server communication. The definition of the same origin is:
- Same protocol
- Same domain
- Same port
Are these two URLs the same origin?
http://example.com
http://sub.example.com
No, because the domain is different although the root domain is the same
example.com.
Database #
ACID #
ACID is a set of properties that guarantee database transactions are reliable and consistent in the presence of
concurrent and failure conditions.
| Term | Explanation | In one word |
|---|---|---|
| Atomicity | Transactions are all done or none | All or nothing |
| Consistency | The database’s integrity is maintained before and after the transaction | Integrity |
| Isolation | Transactions are independent of each other | Concurrency safe |
| Durability | Once a transaction is committed, it is permanent | Persistence |
Isolation Levels #
Isolation level is a concept of database transaction concurrency, defining the degree of isolation between
transactions.
- Read Uncommitted
- Read Committed
- Repeatable Read
- Serializable
Concurrency Anomalies #
These three phenomena are database transaction concurrency problems caused by different isolation levels.
| Phenomenon | Description | Isolation-level required |
|---|---|---|
| Dirty Read | Read uncommitted transactions | Read-Committed |
| Unrepeatable Read | The second read in one transaction yields a different result due to another concurrent committed update on the same row | Repeatable Read |
| Phantom Read | The second read in one transaction got a different number of results due to another concurrent committed insert/delete transaction | Serializable |
Database Security #
- Place the database in a private subnet and only allow specific IP addresses to access it.
- Separate the database and application server networks.
- Use strong passwords, change them regularly, and minimize exposure.
- Encrypt data during transmission and storage.
Index #
Composite Index #
With the following table structure and index, the table has tens of millions of rows.
1CREATE TABLE users
2(
3 a INT,
4 b INT,
5 c INT
6);
7
8CREATE INDEX idx ON users (a, b, c);
Will the following query use the index?
1SELECT *
2FROM users
3WHERE a > 1
4ORDER BY c;
No
According to the leftmost matching principle, the first field of the index is
a, but the query condition is a single-sided range selectiona > 1, which is not an exact match and the range is too large, so the index will not be used.
Development #
Heap #
A heap is a complete binary tree in which each node’s value is greater than or equal to its child nodes’ values. If
the root node’s value is the largest, it is a max heap; if the root node’s value is the smallest, it is a min heap.
- Insertion and deletion time complexity is \(O(\log n)\).
- Querying the maximum/minimum value time complexity is \(O(1)\).
Whenever you need to quickly find the maximum or minimum value, consider using a heap, such as a priority queue, Dijkstra’s algorithm, heap sort, etc.
Stack #
A stack is a data structure that follows the first-in, last-out (FILO) principle and can only insert and delete at the
top of the stack.
- Insertion and deletion time complexity is \(O(1)\).
- Query time complexity is \(O(n)\).
Whenever you need to reverse the order of elements, consider using a stack, such as function calls, expression evaluation, bracket matching, etc.
Race Condition #
A race condition is a situation in which the result is inconsistent due to the uncertain execution order of multiple
threads or processes.
- Inconsistent data, different results each time.
- Deadlock or illegal data state.
- Difficult to reproduce and debug.
A bad example:
1package main
2
3import (
4 "fmt"
5 "time"
6)
7
8func main() {
9 result := 0
10 for i := 0; i < 10; i++ {
11 go func() {
12 result = i
13 }()
14 }
15 time.Sleep(time.Millisecond)
16 fmt.Println(result)
17}
The key is that the execution order is uncertain, not always wrong, for example, sometimes executed correctly in the order 1-2-3, sometimes chaotic.
The correct way to write:
1package main
2
3import (
4 "fmt"
5 "sync"
6)
7
8var wg sync.WaitGroup
9
10func main() {
11 result := 0
12 for i := 0; i < 10; i++ {
13 wg.Add(1)
14 go func(i int) {
15 result = i
16 wg.Done()
17 }(i)
18 wg.Wait()
19 }
20 fmt.Println(result)
21}
The key is synchronization to ensure order.
Design Patterns #
A design pattern is a summary of common problems in software design and the experience of solving them. Commonly used
patterns include:
- Factory
- Singleton
- Strategy
- Adapter
- Template
Here are two design patterns that I think are commonly used in work: Singleton and Strategy.
Singleton #
The Singleton pattern is a creational design pattern that ensures a class has only one instance and provides a global
access point. Here is the implementation in Go.
1package main
2
3import "sync"
4
5type Singleton struct{}
6
7var (
8 s *Singleton
9 mu sync.Mutex
10)
11
12func Get() *Singleton {
13 if s == nil {
14 mu.Lock()
15 defer mu.Unlock()
16
17 if s == nil {
18 s = &Singleton{}
19 return s
20 }
21 return s
22 }
23 return s
24}
The key is to check if it is empty and lock it for the first time, and then check if it is empty again, rather than creating it directly, otherwise it may be created twice before the lock is completed.
A more modern implementation is to use sync.Once to ensure thread safety, eliminating more cumbersome if judgments.
1package main
2
3import "sync"
4
5type Singleton struct{}
6
7var (
8 s *Singleton
9 once sync.Once
10)
11
12func Get() *Singleton {
13 once.Do(func() {
14 s = &Singleton{}
15 })
16 return s
17}
Strategy #
The Strategy pattern is a behavioral design pattern that defines a series of algorithms, encapsulates each algorithm
into a separate class, and allows them to be replaced. Here is the implementation in Go.
1package main
2
3import "fmt"
4
5type Strategy interface {
6 Do()
7}
8
9type StrategyA struct{}
10
11func (s *StrategyA) Do() {
12 fmt.Println("Strategy A")
13}
14
15type StrategyB struct{}
16
17func (s *StrategyB) Do() {
18 fmt.Println("Strategy B")
19}
20
21type Context struct {
22 strategy Strategy
23}
24
25func (c *Context) SetStrategy(s Strategy) {
26 c.strategy = s
27}
28
29func (c *Context) Execute() {
30 c.strategy.Do()
31}
32
33func main() {
34 context := &Context{}
35
36 if true {
37 context.SetStrategy(&StrategyA{})
38 context.Execute()
39 } else {
40 context.SetStrategy(&StrategyB{})
41 context.Execute()
42 }
43}
The key is to encapsulate the algorithm into a separate class and allow it to be replaced dynamically, rather than hardcoding it.
Algorithm #
Exponentiation by Squaring #
Exponentiation by Squaring is an algorithm for calculating \(a^b\), with a time complexity of \(O(\log b)\). It is a
very test of understanding of bitwise operations and binary. Taking \(a^{13}\) as an example, the binary is 1101.
So
$$ a^{13} = a^{2^3 + 2^2 + 0\cdot2^1 + 2^0} = a^{2^3} \cdot a^{2^2} \cdot a^{0\cdot2^1} \cdot a^{2^0} $$Starting from the right, if the binary bit is 1, the result needs to be multiplied by the corresponding \(a^{2^i}\), otherwise skip it.
- The \(i = 0\) bit is 1, the result is multiplied by \(a^{2^0}\).
- The \(i = 1\) bit is 0, skip it.
- The \(i = 2\) bit is 1, the result is multiplied by \(a^{2^2}\).
- The \(i = 3\) bit is 1, the result is multiplied by \(a^{2^3}\).
Using Golang as an example, the iterative method is preferred:
1package main
2
3func Pow(a float64, b int) float64 {
4 if b < 0 {
5 a, b = 1/a, -b
6 }
7
8 // iterative method
9 var res float64 = 1
10 for b > 0 {
11 if b&1 == 1 {
12 res *= a
13 }
14 a *= a
15 b >>= 1 // b = b / 2
16 }
17 return res
18}
Test cases:
| a | b | res |
|---|---|---|
| any | 0 | 1 |
| 0 | any | 0 |
| 2 | 10 | 1024 |
| 2 | -10 | 0.0009765625 |
The implementation can be iterative or recursive, but the iterative method is superior. If the algorithm \(O(\log b)\) is not implemented, it is unqualified.
DevOps #
VSZ VS RSS #
VSZ(Virtual Set Size) is the total virtual memory allocated to the process, including the code segment, data segment, heap, and stack.RSS(Resident Set Size) is the actual physical memory (RAM) currently being used by the process, including the code segment, data segment, and heap.
| Metrics | VSZ | RSS |
|---|---|---|
| Definition | Total virtual memory allocated to the process | Actual physical memory (RAM) currently being used by the process |
| Scope | All virtual memory, including swapped memory, memory-mapped files, and shared memory | Only the pages of the process currently in physical RAM |
| Size | Larger | Smaller |
| Use Case | Show memory usage of all time | Realtime RAM usage |
Check the VSZ and RSS of a process #
1ps -eo pid,%mem,vsz,rss,comm | grep <process_name>
Check the top ten processes with the highest real-time memory usage #
1ps -eo pid,%mem,vsz,rss,comm | sort -nk2 -r | head -n 10
Architecture #
Cloud Computing #
What is Availability Zone (AZ)? #
An Availability Zone is an isolated data center, usually located in the same geographical region but physically
isolated so that a failure in one AZ does not affect another.
Rate limiting #
Rate limiting is a method of controlling the number of requests sent to a server within a certain period to prevent or mitigate the service overload caused by excessive requests.
What is a bastion host? #
A Bastion Host is a security tool used to manage and monitor server access. Users access servers through the bastion
host, which records user operations and provides auditing and security.
A bastion host is also called a jump host.
Load Balancing #
Round Robin #
Round Robin is a load balancing algorithm that distributes requests to each server in the server list in turn. For
example, with three servers, requests are distributed to A, B, C, A, B, C, A, B, C… in turn.
Similar algorithms include weighted round-robin, which distributes requests to servers based on server load.
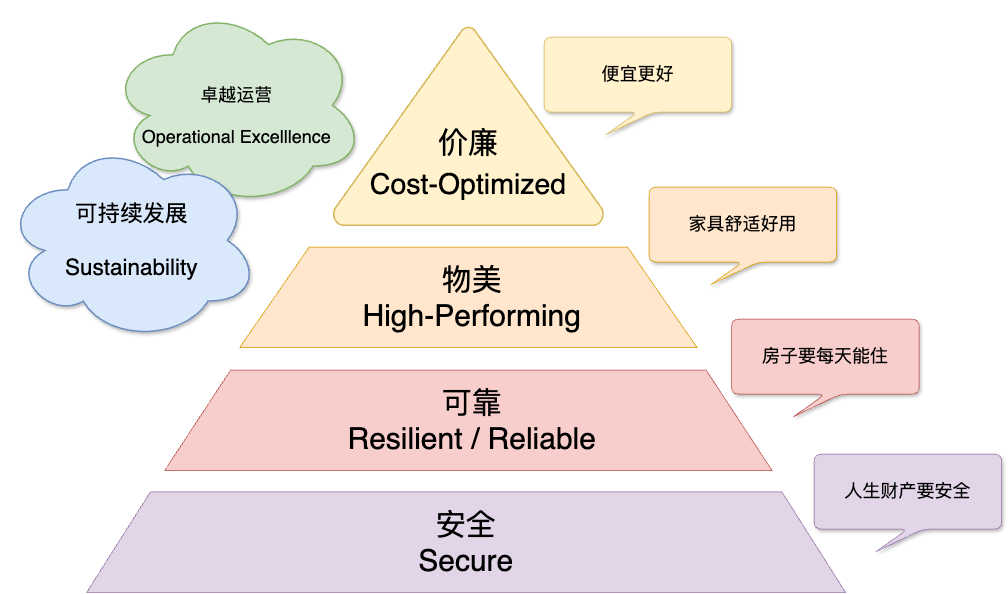
How to evaluate a system #
Four dimensions: security, reliability, performance, and cost.
CDN #
CDN (Content Delivery Network) is a distributed network used to cache and distribute static resources, improving
website performance and user experience.
- Reduce latency by placing resources closer to the client.
- Reduce the network bandwidth and load on the origin server.
- Improve the availability of the origin server.
- Enhance security by preventing DDoS attacks.
CDN is essentially a macro-level cache.
Cybersecurity #
What is a DDoS attack? #
DDoS (Distributed Denial of Service) is a network attack that uses distributed clients to generate a large number of
requests, causing the target service to overload or trigger errors, making the service unavailable.
How to prevent it? #
Set up a firewall, limit access frequency, use a CDN, use DDoS protection services, use an IP blacklist, use CAPTCHA verification.
High Availability #
- Deploy in multiple regions and availability zones.
- Deploy a load balancer in front of the application server.
- Auto-scaling of workloads.
- Disaster recovery redundancy, including passive-active and active-active deployment.
- Comprehensive monitoring and alerting.
Mathematics #
Mainly test basic mathematical knowledge and the ability to solve problems on the spot. Having good mathematical skills is essential for excellent engineers!
Permutation and Combination #
There are 99 people in a room, every two of them will shake hands without duplication. How many handshakes are there in total?
$$ C_n^m = \frac{n!}{m!(n-m)!} $$$$ C_{99}^2 = \frac{99!}{2!(99-2)!} = \frac{99*98}{2} = 99*49 = 4851 $$In a room with 99 people, the first person can shake hands with 98 people, the second person can shake hands with 97 people, and so on. Essentially, it is a permutation and combination of selecting 2 people from 99.
Queue Theory #
In a bank, an average of 100 customers arrive randomly every hour, following a Poisson distribution. The average service time per customer is 100 milliseconds, and only one customer can be served at a time, with no queue. How many customers will be rejected on average in an hour?
$$ \lambda (arrival rate) = \frac{1}{\text{interval of arrival}} = \frac{100}{3600} = \frac{1}{36} $$$$ \mu (service rate) = \frac{1}{\text{service duration}} = \frac{1000}{100 (millisecond)} = 10 $$$$ \rho (utilization rate) = \frac{\lambda}{\mu} = \frac{1}{36*10} = \frac{1}{360} $$$$ \text{average number of denial within one hour} = \lambda * \rho = \frac{1}{360} * 100 = \frac{100}{360} = \frac{5}{18} = 0.2777 $$The M/M/1 queue is a basic queuing model, where M stands for exponential distribution of arrival and service rates, and 1 stands for only one service station.
In the M/M/1 queue model, the rejection rate is equal to the utilization rate, as rejection will occur when the system is utilized.
Topology #
A project has the following dependencies:
A: D
B: A
C: A, D
D: (no dependencies)
E: B, C
How to arrange the execution order of tasks?
Topological sorting, i.e., sorting of a directed acyclic graph (DAG). First, find tasks without dependencies, then delete the task, continue to find tasks without dependencies, until all tasks are deleted.
The order is: D -> A -> B -> C -> E OR D -> A -> C -> B -> E
B and C can be parallel.
Implementation in JavaScript:
1const input = {
2 A: ["D"], // A depends on D
3 B: ["A"],
4 C: ["A", "D"],
5 D: [],
6 E: ["B", "C"],
7}
8
9const indegree = {} // a map to store the indegree of each task
10const queue = [] // queue stores the task that has no indegree (dependency)
11const result = [] // sorted result
12
13// init indegree map
14for (const k in input) {
15 if (input[k].length) {
16 indegree[k] = input[k].length // length of dependencies is the indegree
17 } else {
18 queue.push(k) // if no dependencies, push to the queue
19 }
20}
21
22// until the queue is empty
23while (queue.length) {
24 // take the earliest task from the queue
25 const el = queue[0]
26
27 for (const k in input) {
28 if (input[k].includes(el)) {
29 indegree[k] -= 1
30
31 if (indegree[k] === 0) {
32 queue.push(k)
33 }
34 }
35 }
36
37 // push to the result
38 result.push(el)
39 // remove from the queue
40 queue.shift()
41}
42
43console.log(result) // ["D", "A", "B", "C", "E"]
Discrete Mathematics #
For a general sorting algorithm, what is the lower bound of the time complexity without any assumptions about the data?
$$ \log_2(n!) = \Theta(n \log n) $$Why? Sorting is essentially comparison, which can be represented by a decision tree. The depth of the decision tree is the number of comparisons in the worst case. For sorting \(n\) elements, there are \(n!\) permutations, so the number of leaf nodes in the decision tree is \(n!\), and the height is \(h\), satisfying:
$$ 2^h \geq n! $$$$ h \geq \log_2(n!) $$Based on Stirling’s formula:
$$ \begin{aligned} n! &\approx \sqrt{2\pi n}(\frac{n}{e})^n \\ \log_2(n!) &\approx n \log_2 n - n \log_2 e \\ &\approx n \log_2 n \end{aligned} $$So:
$$ h \geq n \log_2 n $$Statistics #
P50 and P99
P50 is the median, the value in the middle of the data. P99 is the percentile, the value in the top 1% of the data.
Open Questions #
The following questions have no standard answers and test the interviewee’s understanding and depth of their work area.
- What is your most commonly used programming language, and what are its advantages and disadvantages?
- In your last responsible project, how many lines of code were there? How many APIs? How many batch tasks? How many users? What was the maximum RPS?
- How do you persuade others and sell your ideas?
- What are your goals for the next ten years?
- What is the future development direction of engineers?
- What is the biggest mistake you have made?