With a coding scheme where the minimum hamming distance between two valid codewords is m, it can detect r-bit errors at most when
1 + r ≤ m
Or can correct r-bit errors at most when
1 + 2r ≤ m
Why are they true?
Error detection #
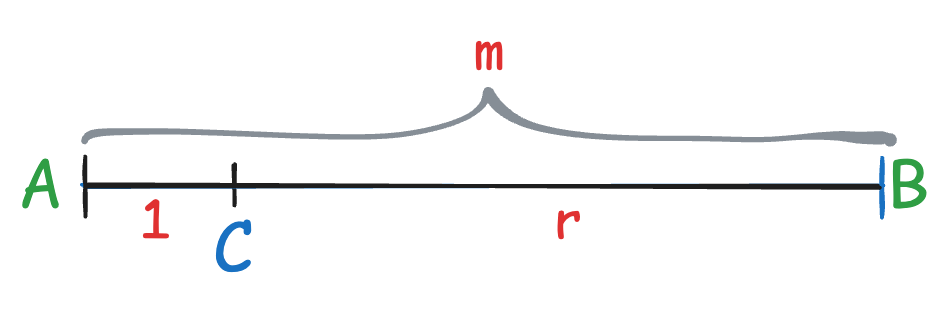
Assume two codewords A and B are defined, and we receive C, which should be one of A and B. Because the maximum distance of C to A or B is only r (i.e., at most r-bit errors), and according to the above inequality, the minimum distance between A and B must be more than r + 1, so the C with r-bit errors will not be mistakenly recognized as any legal codeword. However, we cannot know whether C originally should be A or B because it may come from a 1-bit error starting from A or an r-bit error starting from B.
Error correction #
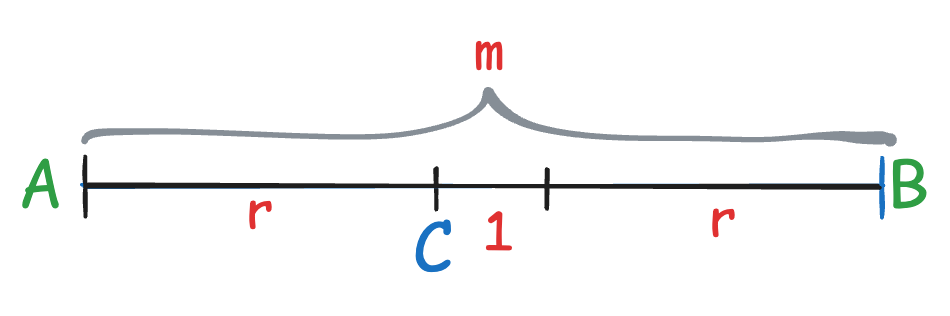
To correct an error, we must be able to tell which valid codeword a corrupted one is closer to. Since A and B can both have maximum r-bit errors, we must have 1 distance further so there will always be a winner. Otherwise, without that 1 additional distance, C could result from r-bit errors from either A or B.
Hamming code #
In the real world, a single bit error is rare, and two bits are even rarer, so the famous Hamming code is designed to correct a single bit error. We learn from the most basic case.
Suppose only one bit is transmitted, there is only one error case, that is, the flip of that single bit. Error detection and correction become the same thing. How many check bits do we need?
If we add one more bit for parity check, we can’t know if the corruption occurs on the message or the redundant bit since it could happen to either one. So, we need a second redundant bit that works the same way — pairing with the message bit to achieve an odd or even parity check. Since there could be only one error, we have three possibilities when an error occurs:
- The message bit is corrupted.
- The first check bit is corrupted.
- The second check bit is corrupted.
For these three cases, we have clear answers:
- If the message bit flips, the other two parity check bits must have the same value since they each pair with the message bit.
- If the first check bit flips, the message bit and the second check bit must match the parity check.
- Likewise, if the second check bit flips, the message bit and the first check bit must match the parity check.
The number of check bits needed to correct a single bit error #
In general, from the information theory perspective, the minimum number of check bits r needed to detect a single bit error in m bits of information.
1 + r + m ≤ 2^r
Because since the total width of a codeword is r + m and each bit could be wrong (though the total number of errors can only be 1), there are r + m error states. Besides, there is a “no error” state. So, there are 1 + r + m states to distinguish. It is obvious that r check bits can express 2^r states, thus we get the above formula.