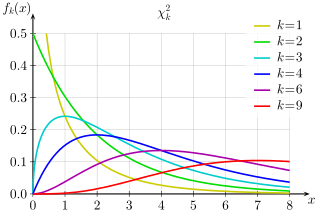
卡方分布形态为右偏,形状由自由度 \(\nu\) 决定。
定义 #
假设有一组独立随机变量 \(Z_1, Z_2, \ldots, Z_{\nu}\),它们都服从标准正态分布 \(N(0, 1)\)。即每个变量的期望值为 \(0\),方差为 \(1\)。那么这些变量的平方和服从自由度为 \(\nu\) 的卡方分布:
$$ Q = Z_1^2 + Z_2^2 + \ldots + Z_{\nu}^2 = \sum_{i=1}^{\nu} Z_i^2 $$那么这个平方和 \(Q\) 就服从自由度为 \(\nu\) 的卡方分布:
$$ Q \sim \chi^2(\nu) $$显然,卡方分布是非负的,因为平方和不可能为负数。
“卡方”(Chi-Square)得名于希腊字母 𝜒(Chi),表示统计学中常用的平方和统计量。
自由度 #
自由度 \(\nu\) 是独立变量的个数。即可以独立变化的信息的维度数。自由度越大,说明背后的独立因素越多,加和就越接近正态分布。因为这正是中心极限定理导致的,也是正态分布的核心意义。
- \(\nu = 1\) 时:就是指数分布。非常偏态。
- \(\nu = 3\) 时:偏度(Skewness)减少,峰值向右移动。
- …
- \(\nu \geq 30\) 时:近似正态分布。
简而言之,大量独立变量的平方和趋近正态分布。
右偏分布 #
卡方分布具有偏态性,即右偏,也叫正偏。意思是有又平又长的尾巴,小值(接近 \(0\))概率较高。随着变量值增大,概率密度逐渐减小。特征是:
均值 > 中位数 > 众数
众数是指数据集中出现次数最多的数值。
期望和方差 #
期望 #
期望等于自由度 \(\nu\),推导如下(利用期望的线性性质):
$$ \begin{aligned} E(Q) &= E(Z_1^2 + Z_2^2 + \ldots + Z_{\nu}^2) \\ &= E(Z_1^2) + E(Z_2^2) + \ldots + E(Z_{\nu}^2) \\ &= 1 + 1 + \ldots + 1 \\ &= \nu \end{aligned} $$为什么 \(E(Z_i^2) = 1\)?首先,通过方差的定义:
$$ Var(Z_i) = E(Z_i^2) - E(Z_i)^2 $$参见:理解方差
所以:
$$ E(Z_i^2) = Var(Z_i) + E(Z_i)^2 $$而每个 \(Z_i\) 都来源于标准正态分布,即:
$$ Z_i \sim N(0, 1) $$所以:
$$ \begin{aligned} E(Z_i) = 0 \\ Var(Z_i) = 1 \end{aligned} $$代入得到:
$$ E(Z_i^2) = Var(Z_i) + E(Z_i)^2 = 1 + 0 = 1 $$方差 #
由于方差的可加性(线性性质):
$$ \begin{aligned} Var(Q) &= Var(Z_1^2 + Z_2^2 + \ldots + Z_{\nu}^2) \\ &= Var(Z_1^2) + Var(Z_2^2) + \ldots + Var(Z_{\nu}^2) \\ \end{aligned} $$对于每个 \(Z_i^2\),利用方差的定义:
$$ Var(Z_i^2) = E(Z_i^4) - E(Z_i^2)^2 $$为什么要平方和? #
- 平方消除了正负号,强调了绝对值。
- 平方放大了离均值较远的值,强调了离散程度。
- 可直接用于推导和检验方差。
- 平方导致非负值,这对统计检验尤为重要。
如果不平方,多个正太分布变量的和依旧是正态分布。