具有有限均值和方差的任何分布,样本均值的分布都会接近正态分布。即中心极限定理(Central Limit Theorem)。
因此,宇宙中,由许多微小独立随机因素影响的量,可以被认为具有正态分布。
样本均值 #
对任何一个有期望 \( \mu \) 和方差 \( \sigma^2 \) 的随机变量 \( X \),在抽取 \( n \) 个样本的情况下,样本均值的期望值为:
$$ E(\bar{X}) = \mu $$因为首先,样本均值 \(\bar{X}\) 是所有样本的平均值:
$$ \bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i $$每个样本 \(X_i\) 是独立同分布的,期望值 \(E(X_i) = \mu\),所以:
$$ E[\bar{X}] = \frac{1}{n} \sum_{i=1}^{n} E[X_i] = \frac{1}{n} n \mu = \mu $$大数法则 (Law of Large Numbers): 样本均值随着样本数量的增加,会逐渐接近总体均值。
样本方差 #
样本方差的期望值为:
$$ Var(\bar{X}) = \frac{\sigma^2}{n} $$因为:
$$ \begin{align} Var(\bar{X}) &= Var(\frac{1}{n} \sum_{i=1}^{n} X_i) \\ &= \frac{1}{n^2} \sum_{i=1}^{n} Var(X_i) \\ &= \frac{1}{n^2} n \sigma^2 = \frac{\sigma^2}{n} \end{align} $$此处用到了方差的数乘性质:\( Var(aX) = a^2 Var(X) \)
正态分布 #
正态分布是自然界中最常见的分布之一,是最“自然”的分布。它描述大量独立事件叠加后的结果,是随机变量加和的极限分布。原因是这种分布的熵最大,也就是说,它携带的信息最少,具有最少的假设和最简单的形状。
许多自然和社会现象都是大量独立因素叠加的结果,比如气温、人的身高、成绩等。
概率密度函数 (Probability Density Function) 为:
$$ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$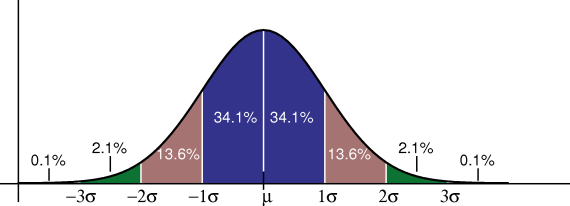
正态分布拥有所谓的 68-95-99.7 规则,即在均值 \( \mu \) 附近的 1、2、3 个标准差内分别包含了 68%、95%、99.7% 的数据。
为何趋于正态分布? #
随着样本数量 \( n \) 的增加,每个样本带来的波动性相互抵消,使整个系统的波动性逐渐减小,使得样本均值的分布逐渐接近正态分布。因为正态分布就是加和随机变量的极限分布。