Collisions in Poisson Process

November 12, 2024

Study

This is problem that you may encounter, and I found a simple way to calculate it. The result looks correct after comparing with the actual data. A website receives an average of 1000 requests per hour, and can only handle one at a time, taking 1 second. When a request arrives, if the previous one has not been completed, an error will occur. How many errors will occur on average in an hour?

By treating website traffic as a Poisson process, the result can be calculated.

Poisson Process #

A Poisson process is a random process in which events occur at a constant rate:

The number of events in a unit time follows a Poisson distribution.
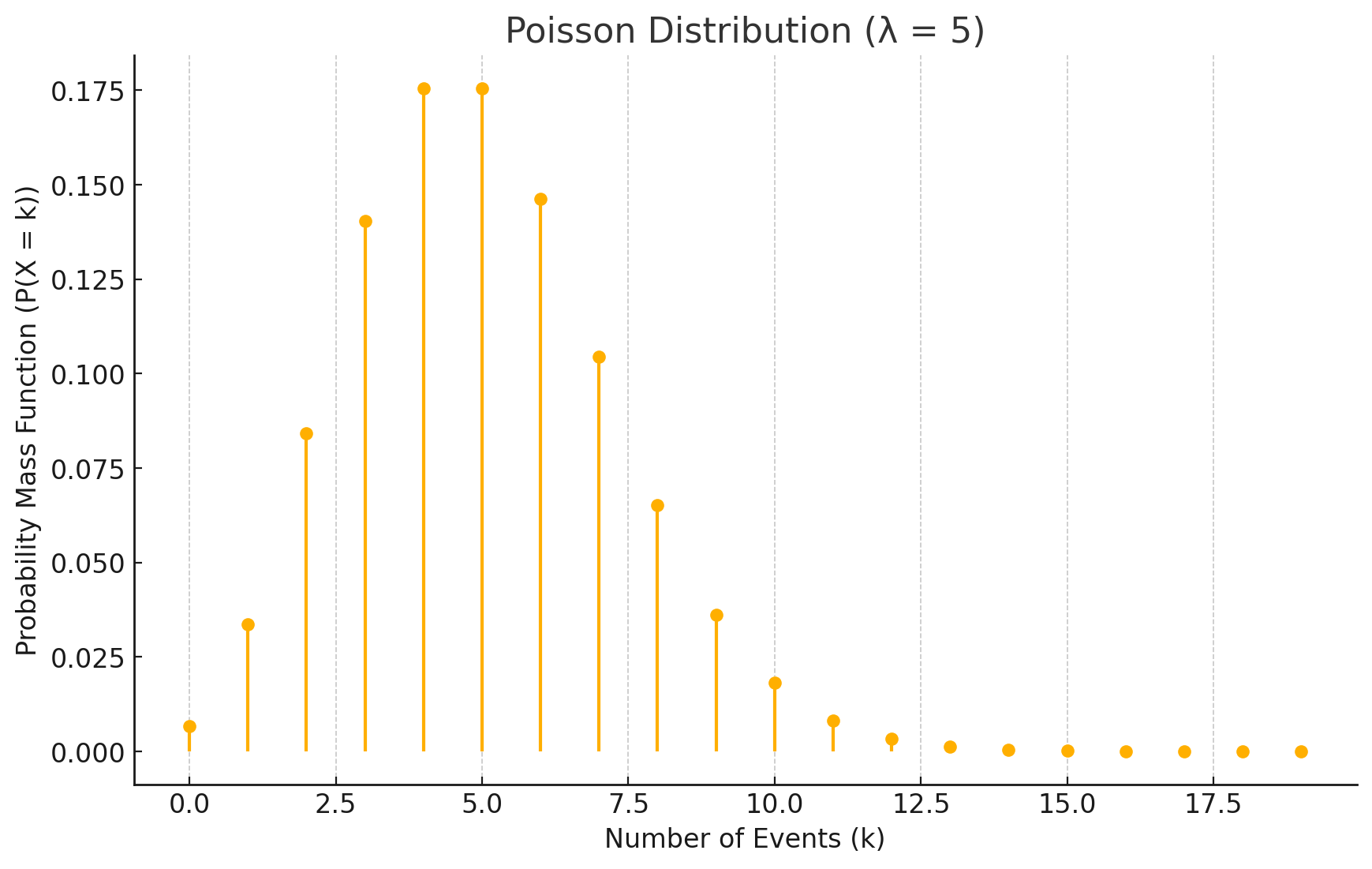
The time interval follows an exponential distribution.

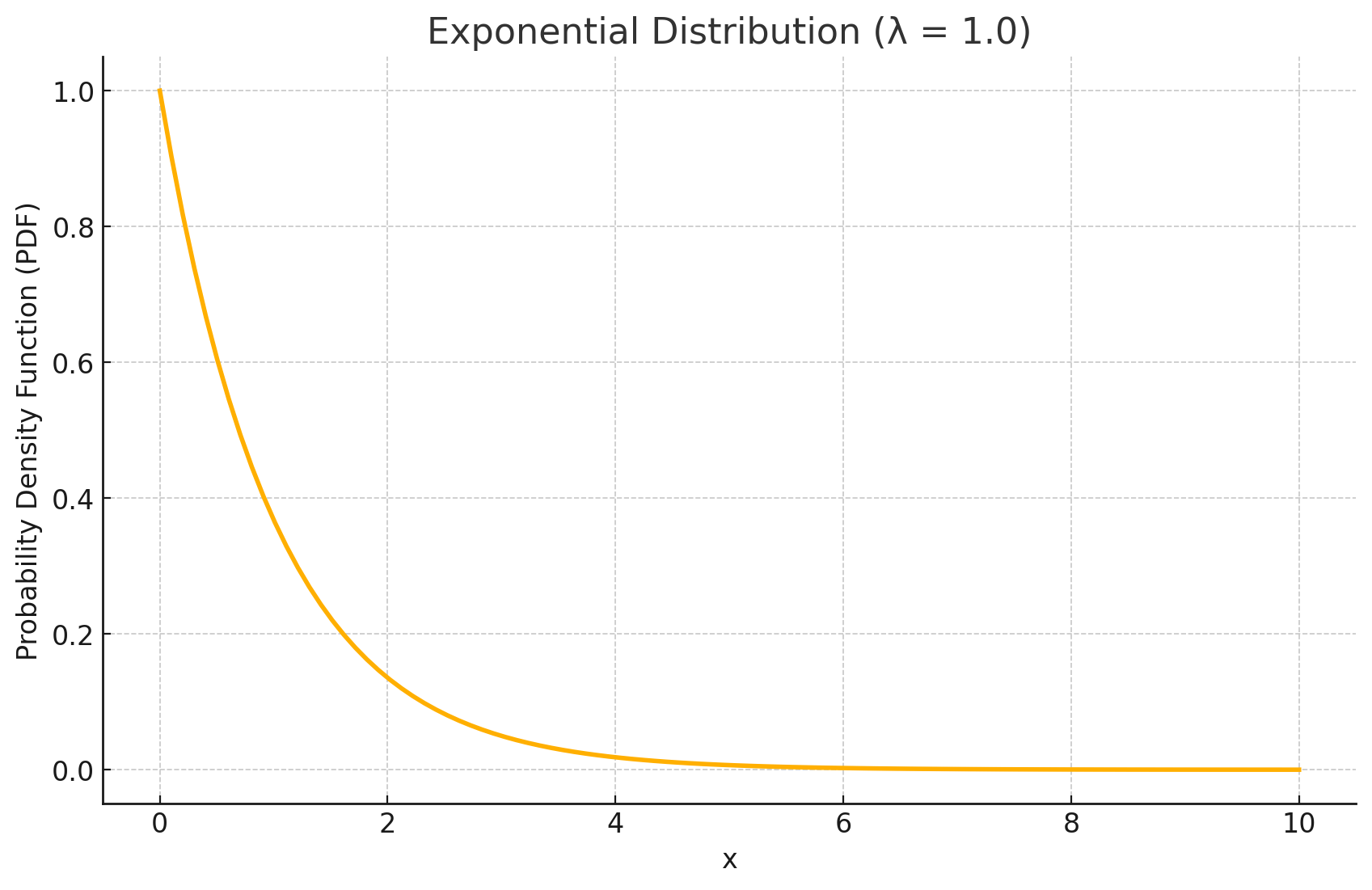
Derivation #

Below is the well-known binomial distribution, where $P (X = k)$ represents the probability of $k$ successes in $n$ trials.

P (X = k) = C_{n}^{k} p^{k} (1 - p)^{n - k}

Its limit expression equals the probability mass function (PMF) of the Poisson distribution, because it originates from the binomial distribution, so it is also discrete. Its meaning is the probability of $k$ events occurring in a unit time when the rate of occurrence is constant.

lim_{n \to \infty} C_{n}^{k} p^{k} (1 - p)^{n - k} = \frac{λ^{k} e^{- λ}}{k!}

Obviously, the probability that no event occurs in a unit time is

P (X = 0) = \frac{λ^{0} e^{- λ}}{0!} = e^{- λ}

So the probability that at least one event occurs in a unit time is

P (X = 0) = e^{- λ t}

Apparently, the probability of at least one event occurring in $t$ unit time is

P (X \geq 1) = 1 - e^{- λ t}

Number of Collisions #

In the real world, a collision is when the next event occurs before the previous one ends. The expected number of collisions can be calculated as follows:

\begin{aligned} E (X) & = (T o t a l r e q u e s t s - 1) \times P (X \geq 1) \\ = (T λ - 1) \times (1 - e^{- λ t}) \end{aligned}

Where $T$ is the time unit, and $λ$ is the rate of occurrence.

The reason why it can be calculated like this is that each event has an equal chance of colliding with the previous event (due to the memorylessness of the exponential distribution), and there are $T λ - 1$ opportunities for such collisions.

Conclusion #

Back to the original question, the duration of a request is 1 second, and there are an average of 1000 requests per hour, so the expected number of collisions is

E (X) = (1000 - 1) \times (1 - e^{- 1000 / 3600}) \approx 0.632

This means that on average, the expected number of collisions in a day is

E (X) = (1000 \times 24 - 1) \times (1 - e^{- 1000 / 3600 \times 24}) \approx 15.17