Matrix multiplication has four cases, but essentially they are all vector operations.
- Vector dot product
- Matrix multiply vector (right multiply)
- Vector multiply matrix (left multiply)
- Matrix multiply matrix
Vector Dot Product #
The dot product is an operation between two vectors, the result is a scalar. Think of it as how far two vectors can go when combined. Simply multiplying the magnitudes is incorrect because vectors have directions. To be collinear, you have to multiply by the cosine of the angle.
$$ \begin{bmatrix} x_1 & y_1 \end{bmatrix} \begin{bmatrix} x_2 \\ y_2 \end{bmatrix} = x_1x_2 + y_1y_2 = |A||B|cos\theta $$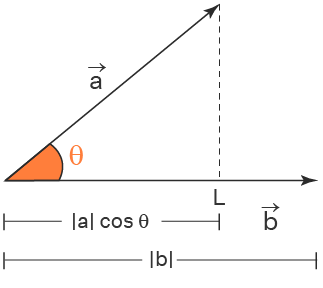
More generally:
$$ a \cdot b = \sum_{i=1}^{n} a_ib_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n $$Matrix Multiply Vector (Right Multiply) #
The meaning is the matrix (left) transforms the vector (right).
$$ \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = x \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + y \begin{bmatrix} y_1 \\ y_2 \end{bmatrix} = \begin{bmatrix} x_1x + y_1y \\ x_2x + y_2y \end{bmatrix} $$\(n \times p\) * \(p \times 1\) = \(n \times 1\)
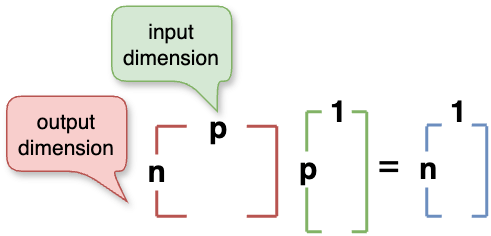
\(n\) in the vector represents the number of dimensions. In the matrix, the columns represent the dimensions of the input vector, and the rows represent the dimensions of the output vector. So the number of columns in the matrix must be equal to the number of rows in the vector; the output dimension \(m\) can be arbitrary.
$$ x_{\text{new}} = \\ \begin{bmatrix} x_1 & y_1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = x_1x + y_1y $$$$ y_{\text{new}} = \\ \begin{bmatrix} x_2 & y_2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = x_2x + y_2y $$Here, it means transforming the input two-dimensional vector into another vector in two-dimensional space. \([x_1, y_1]\) tells how the new component \(x_{\text{new}}\) changes due to the two dimensions. \([x_2, y_2]\) tells how the new component \(y_{\text{new}}\) changes due to the two dimensions. Higher dimensions are similar. The calculation method is the dot product.
$$ Ax = \begin{bmatrix} x_{\text{new}} \\ y_{\text{new}} \end{bmatrix} $$Dimensionality Reduction #
If the matrix has only one row, the output space is one-dimensional, and there is no indication of the change in the second component \(y\). Consequently, the two-dimensional vector input becomes a scalar, and the space changes from a plane to a line (only the length remains).
$$ \begin{bmatrix} x_1 & y_1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = x_1x + y_1y $$Another way to reduce dimensionality is to keep the output space two-dimensional, but the second component is \(0\), so the two-dimensional vector input is projected onto a line in two-dimensional space - the \(x\) axis.
$$ \begin{bmatrix} x_1 & y_1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x_1x + y_1y \\ 0 \end{bmatrix} $$Dimensionality Increase #
Of course, you can increase the dimensionality. Although the vector does not provide information about the third dimension, the new information in the third dimension comes from the weighted sum of the first two dimensions.
$$ \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} x_1x + y_1y \\ x_2x + y_2y \\ x_3x + y_3y \end{bmatrix} $$Vector Multiply Matrix (Left Multiply) #
The meaning is the vector (left) compresses the matrix (right).
\(1 \times p\) * \(p \times m\) = \(1 \times m\)
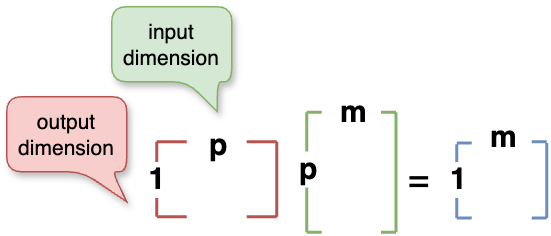
A line vector is equivalent to a matrix with only one row. With the understanding of right multiplication, left multiplication is equivalent to compressing the matrix on the right to one-dimensional output.
$$ \begin{align} \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} x_1 & x_2 \\ y_1 & y_2 \end{bmatrix} &= \begin{bmatrix} \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} x_2 \\ y_2 \end{bmatrix} \end{bmatrix} \\ &= \begin{bmatrix} x_1x + x_2y & y_1x + y_2y \end{bmatrix} \end{align} $$Matrix Multiply Matrix #
The meaning is the matrix (left) transforms the matrix (right).
\(n \times p\) * \(p \times m\) = \(n \times m\)
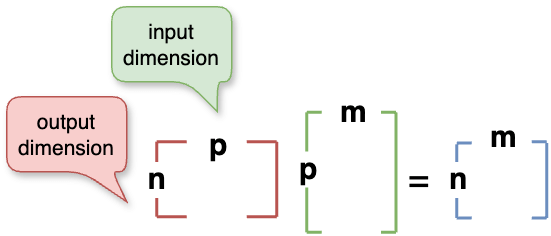
Matrix multiplication is equivalent to linear combinations. Read from right to left, the rightmost matrix is the initial state, transformed by the matrix on the left, and can be concatenated indefinitely. To calculate, consider the right matrix as many column vectors, each transformed by the left matrix and then combined.
$$ \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \end{bmatrix} \begin{bmatrix} a & c \\ b & d \end{bmatrix} = \begin{bmatrix} \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix} \end{bmatrix} = \begin{bmatrix} x_1a + y_1b & x_1c + y_1d \\ x_2a + y2_b & x_2c + y_2d \end{bmatrix} $$Obviously, the input dimension of the leftmost matrix will never change. Because the matrix is a transformation function, the input of the function is fixed, and the output can change. So the continuous multiplication of matrices is equivalent to composite functions.
$$ A = \begin{bmatrix} a_1 & a_2 \\ a_3 & a_4 \end{bmatrix} = f_A(x) $$$$ B = \begin{bmatrix} b_1 & b_2 \\ b_3 & b_4 \end{bmatrix} = f_B(x) $$$$ AB = f_A(f_B(x)) $$\(x\) is any valid (dimensionally consistent) input