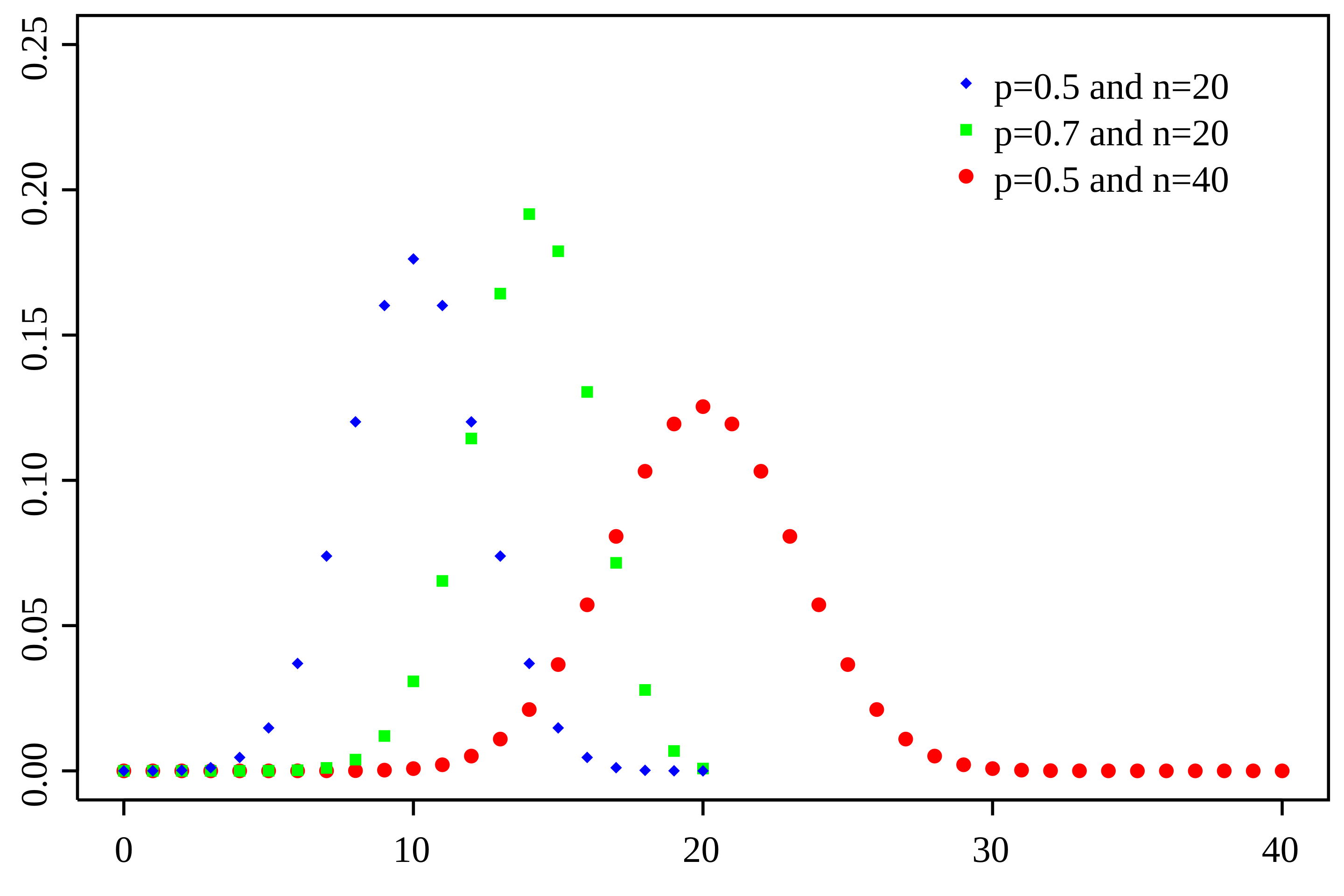
The binomial distribution is the foundation of almost everything, describing the probability distribution of the number of successes \(k\) in \(n\) independent repeated experiments (Bernoulli trials).
Definition #
For \(X ~ B(n, p)\), i.e., the parameter follows a binomial distribution with \(n\) trials and success probability \(p\), the probability mass function is:
$$ P(X=k) = C(n, k) \cdot p^k \cdot (1-p)^{n-k} $$Repeated Independent Trials (Bernoulli Trials) #
It is a random experiment with only two results, such as flipping a coin, either heads or tails, either win or lose. And the probability of success is the same each time, i.e., the previous one does not affect the next one.

Probability Mass Function (PMF) #
The Probability Mass Function (PMF) is the probability of a discrete random variable at each value. The sum of all values is 1.
$$ \sum_{x=0}^{n} P(X) = 1\ $$Derivation #
The success probability is \(p\), the failure probability is \(1-p\), and now we do \(n\) trials.
The probability of all successes is:
$$ P(X=n) = p^n $$The probability of all failures (i.e., the number of successes is \(0\)) is:
$$ P(X=0) = (1-p)^n $$The probability of succeeding \(1\) time is to select 1 success from \(n\) trials.
$$ P(X=1) = C(n, 1) \cdot p \cdot (1-p)^{n-1} $$So the probability of succeeding \(k\) times is to select \(k\) successes from \(n\) trials.
$$ P(X=k) = C(n, k) \cdot p^k \cdot (1-p)^{n-k} $$$$ C(n, k) = \frac{n!}{k!(n-k)!} $$The combination used above is the total number of ways to select \(k\) elements from \(n\) elements, denoted as \(C(n, k)\).
For example, selecting \(1\) from \(n\) elements obviously has \(n\) ways, i.e., \(C(n, 1) = n\).
Expectation (Average Number of Successes) #
Intuitively, the number of experiments multiplied by the probability of success is the expected value. Why? For a single Bernoulli experiment, i.e., the expected value of each \(X_i\) is \(p\). Because either success or failure:
$$ E(X_i) = 1 \cdot p + 0 \cdot (1-p) = p $$By using the linearity of expectation, the expected value of \(n\) experiments is \(np\).
$$ E(X) = E(\sum_{i=1}^{n} X_i) = \sum_{i=1}^{n} E(X_i) = np $$Variance #
Variance describes the degree of fluctuation of the number of successes around the expected value \(np\), defined as the mean of the square of the differences between each data point and the mean.
$$ Var(X) = E[(X - E[X])^2] $$When expanded, we get the following formula, which is easier to derive the variance of the binomial distribution. (See previous: Understanding Variance)
$$ Var(X) = E(X^2) - E(X)^2 $$The variance of the binomial distribution is:
$$ Var(X ~ B(n, p)) = np(1-p) $$Why? For a single Bernoulli variable (the result of a single Bernoulli experiment) because \(X_i\) can only be \(0\) or \(1\), so:
$$ X_i^2 = X_i $$This can be verified by substituting \(X_i = 0\) and \(X_i = 1\).
So
$$ E(X_i^2) = E(X_i) = p $$Since the expectation of a single variable is known, i.e., \(E(X_i) = p\), the variance of a single variable is:
$$ Var(X_i) = E(X_i^2) - E(X_i)^2 = p - p^2 = p(1-p) $$By using the linearity of variance, the variance of \(n\) experiments is:
$$ Var(X) = Var(\sum_{i=1}^{n} X_i) = \sum_{i=1}^{n} Var(X_i) = np(1-p) $$Intuition of Variance #
An important intuition is that because there is \(p(1-p)\), when \(p = 0.5\), the variance is the largest. Obviously, the uncertainty represented by a 50% success rate is the highest. Similarly, in a rectangle with a fixed perimeter, the area of a square is the largest.
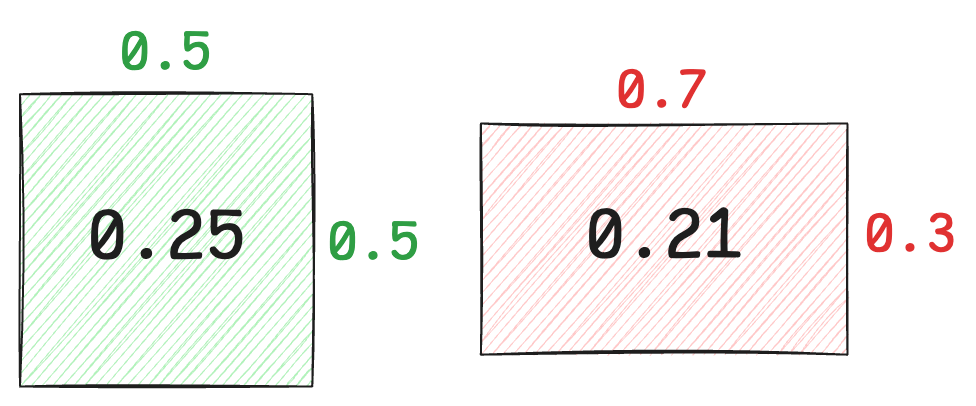
If the success rate is 0% or 100%, there will be no fluctuation, i.e., a certain event, no randomness, so the variance is 0. That is, the rectangle has one side of zero, and the area is also zero.
Standard Deviation #
The standard deviation is the square root of the variance. So obviously:
$$ \sigma = \sqrt{np(1-p)} $$